
This page contains the Learning and Assessment Framework (LAF). The LAF has eight zones: Primitive Modelling, Intuitive Modelling, Sensing, Strategy Exploring, Strategy Refining, Strategy Extending, Connecting and Reflective Knowing.
In the descriptors of each of these zones, reference is made to the assessment tasks that are contained in Booklets 1 and 2 of the original SNMY. These may be accessed here.
In the table below the LAF, the zones are mapped to the Australian Curriculum: Mathematics. It can be seen that there is a broad alignment between the zones and the year levels.
The updated version of the National Numeracy Learning Progression (NNLP) has not yet been published. After publication, we will include a mapping between the LAF and the NNLP.

Learning and Assessment Framework
Zone Description
Primitive Modelling
Can solve simple multiplication and division problems involving relatively small whole numbers.
For example, Butterfly House parts a and b. Tends to rely on drawing, models and count-all strategies.
For example, draws and counts all pots for part a of Packing Pots. May use skip counting (repeated addition) for groups less than 5.
For example, to find number of tables needed to seat up to 20 people in Tables and Chairs. Can make simple observations from data given in a task.
For example, Adventure Camp a. Can reproduce a simple pattern.
For example, Tables and Chairs, parts a to e. Multiplicative Thinking (MT) not really apparent as there is no indication that groups are perceived as composite units, dealt with systematically, or that the number of groups can be manipulated to support a more efficient calculation.
Can make simple observations from data given in a task (e.g. Adventure Camp a) and reproduce a simple pattern (e.g. Tables and Chairs a to e)
Multiplicative thinking (MT) not really apparent as no indication that groups are perceived as composite units, dealt with systematically, or that the number of groups can be manipulated to support a more efficient calculation
* these items are from the original SNMY research
Teaching Implications
Consolidate/establish:
Trusting the count for numbers to 10 (e.g. for 6 this involves working with mental objects for 6 without having to model and/or count-all). Use flash cards to develop subitising (i.e. ability to say how many without counting) for numbers to 5 initially and then to 10 and beyond using part-part-whole knowledge (e.g. 8 is 4 and 4, or 5 and 3 more, or 2 less than 10). Practice regularly
Simple skip counting to determine how many in a collection and to establish numbers up to 5 as countable objects, for example, count by twos, fives and tens, using concrete materials and a 0-99 Number Chart
Mental strategies for addition and subtraction facts to 20 for example, Count on from larger (e.g. for 2 and 7, think, 7, 8, 9), Double and near doubles (e.g. use ten- frames and a 2-row bead-frame to show that 7 and 7 is 10 and 4 more, 14), and Make-to-ten (e.g. for 6 and 8, think, 8, 10, 14, scaffold using open number lines). Explore and name mental strategies to solve subtraction problems such as 7 take 2, 12 take 5, and 16 take 9. Practice (e.g. by using Number Charts from Maths 300)
2-digit place-value – working flexibly with ones and tens by making, naming, recording, comparing, ordering, counting forwards and backwards in place-value parts, and renaming. Play the ‘Place-Value Game’ (see Siemon et al, 2015)
Introduce/develop:
Doubling (and halving) strategies for 2-digit numbers that do not require renaming (e.g. 34 and 34, half of 46), build to numbers that require some additional thinking (e.g. to double 36, double 3 tens, double 6 ones, 60 and 12 ones, 72)
Extended mental strategies for addition and subtraction, use efficient, place-value based strategies (e.g. 37 and 24, think: 37, 47, 57, 60, 61). Use open number lines to scaffold thinking
Efficient and reliable strategies for counting large collections (e.g. count a collection of 50 or more by 2s, 5s or 10s) with a focus on how to organise the number of groups to facilitate the count (e.g. by arranging the groups systematically in lines or arrays and then skip counting)
How to make, name and use arrays/regions to solve simple multiplication or sharing problems using concrete materials, and skip counting (e.g. 1 four, 2 fours, 3 fours …), leading to more efficient counting strategies based on reading arrays in terms of a consistent number of rows (e.g. 4 rows of anything, that is, 4 ones, 4 twos, 4 threes, 4 fours, …)
3-digit place-value – working flexibly with tens and hundreds (by making with MAB, naming, recording, comparing, ordering, counting forwards and backwards in place- value parts, and renaming – see Siemon et al, 2015)
Strategies for unpacking and comprehending problem situations (e.g. read and re- tell, ask questions such as, What is the question asking? What do we need to do? …). Use realistic word problems to explore different ideas for multiplication and division. For example, 3 rows, 7 chairs in each row, how many chairs (array)? Mandy has three times as many…as Tom…, how many … does she have (scalar idea)? 24 cards shared among 6 students, how many each (partition)? Lollipops cost 5c each, how much for 4 (‘for each’ idea)?
How to explain and justify solution strategies orally and in writing through words and pictures (important for mathematical literacy)
Zone Description
Intuitive Modelling
Trusts the count for groups of 2 and 5, that is, can use these numbers as units for counting.
For example, Tables & Chairs part j, Butterfly House part d. Counts large collections efficiently and systematically keeps track of count (for example, may order groups in arrays or as a list) but needs to ‘see’ all groups.
For example, Tiles, Tiles, Tiles part a, Butterfly House part e. May use list and/or doubling as follows: 2 butterflies 5 drops 4 butterflies 10 drops 6 butterflies 15 drops … 12 butterflies 30 drops Can share collections into equal groups/parts.
For example, Pizza Party parts a and b. Recognises small numbers as composite units.
For example, can count equal group and skip count by twos, threes and fives Recognises multiplication is relevant, but tends not to be able to follow this through to solution.
For example, Packing Pots part c, Speedy Snail part a. Can list some of the options in simple Cartesian product situations.
For example, Canteen Capers part a. Orders 2 digit numbers.
For example, partially correct ordering of times in Swimming Sports part a. Some evidence of multiplicative thinking as equal groups or shares are
Teaching Implications
Consolidate/establish:
See the Ideas and strategies introduced/developed in the previous Zone
Introduce/develop:
More efficient strategies for counting groups based on a change in focus from a count of equal groups (e.g. (1 three, 2 threes, 3 threes, 4 threes, …) to a consistent number of groups (e.g. 3 ones, 3 twos, 3 threes, 3 fours, …) which underpin the more efficient mental strategies listed below and ultimately lead to the factor-factor- product idea
Array/region-based mental strategies for multiplication facts to 100 for example, doubling (for 2s facts), doubling and 1 more group (for 3s facts), double doubles (for 4s facts), relate to tens (for 5s and 9s facts) and so on (see There’s More to counting Than Meets the Eye)
Efficient strategies for solving problems where arrays and regions only partially observed
 Commutativity, by exploring the relationship between arrays and regions such as 3 fours and 4 threes. Play ‘Multiplication Toss’
Commutativity, by exploring the relationship between arrays and regions such as 3 fours and 4 threes. Play ‘Multiplication Toss’
Informal division strategies such as think of multiplication and halving, (e.g. 16 divided by 4, think: 4 ‘whats’ are 16? 4; or half of 16 is 8, half of 8 is 4)
Extended mental strategies for multiplication (e.g. for 3 twenty-fives, Think: double 25, 50, and twenty-five more, 75) and use place-value based strategies such as 10 groups and 4 more groups for 14 groups
Simple proportion problems involving non-numerical comparisons (e.g. If Nick mixed less cordial with more water than he did yesterday, his drink would taste (a) stronger, (b) weaker (c) exactly the same, or (d) not enough information to tell)
How to recognise and describe simple relationships and patterns (e.g. ‘double and add 2’ from models, diagrams and tables; or notice that a diagonal pattern on a 0-99 chart is a count of 11, 1 ten and 1 ones)
Language of fractions through practical experience with both continuous and discrete, ‘real-world’ fraction models for example, 3 quarters of the pizza, half the class), distinguish between how many and how much (e.g. in 2 thirds the numeral indicates how many, the name indicates how much)
Halving partitioning strategy, through paper folding (kinder squares and streamers), cutting plasticine ‘cakes’ and ‘pizzas’, sharing collections equally (counters, cards etc), apply thinking involved to help children create their own fraction diagrams. Focus on making and naming parts in the halving family (e.g. 8 parts, eighths) including mixed fractions (e.g. “2 and 3 quarters”) and informal recording (e.g. 3 eighths), no symbols
Key fraction generalisations – that is, that equal parts are necessary and that the number of parts names the part
Zone Description
Sensing
Demonstrates intuitive sense of proportion and partitioning.
For example, Butterfly House part f (partial solution), Missing Numbers part b. Works with ‘useful’ numbers such as 2 and 5, and strategies such as doubling and halving.
For example, Packing Pots part b, Pizza Party part c. May list all options in a simple Cartesian product situation but cannot explain or justify solutions.
For example, Canteen Capers part b. Uses abbreviated methods for counting groups. Uses doubling and doubling again to find 4 groups of, or repeated halving to compare simple fractions.
For example, Pizza Party part c. Beginning to work with larger whole numbers and patterns but tends to rely on count all methods or additive thinking to solve problems.
For example, Stained Glass Windows parts a and b, Tiles, Tiles, Tiles part c.
Teaching Implications
Consolidate/establish:
See the Ideas and strategies introduced/developed in the previous Zone.
Introduce/develop:
Place-value based strategies for informally solving problems involving single-digit by two-digit multiplication (e.g. for 3 twenty-eights, THINK, 3 by 2 tens, 60 and 24 more, 84) mentally or in writing
Initial recording to support place-value for multiplication facts (see Siemon et al, 2015 and There’s More to Counting Than Meets the Eye)
More efficient strategies for solving number problems involving simple proportion (e.g. recognise as two-step problems, What do I do first? Find value for common amount. What do I do next? Determine multiplier/factor and apply. Why?)
How to rename number of groups (e.g. think of 6 fours as 5 fours and 1 more four), Practice (e.g. by using ‘Multiplication Toss Game’). Re-name composite numbers in terms of equal groups (e.g. 18 is 2 nines, 9 twos, 3 sixes, 6 threes)
Cartesian product or for each idea using concrete materials and relatively simple problems such as 3 tops and 2 bottoms, how many outfits, or how many different types of pizzas given choice of small, large, medium and 4 varieties? Discuss how to recognise problems of this type and how to keep track of the count such as draw all options, make a list or a table (tree diagrams appear to be too difficult at this level, these are included in Zone 5)
How to interpret problem situations and solutions relevant to context (e.g. Ask, What operation is needed? Why? What does it mean in terms of original question?)
Simple, practical division problems that require the interpretation of remainders relevant to context
Practical sharing situations that introduce names for simple fractional parts beyond the halving family (e.g. thirds for 3 equal parts/shares, sixths for 6 equal parts etc) and help build a sense of fractional parts, for example, 3 sixths is the same as a half or 50%, 7 eighths is nearly 1, “2 and 1 tenth” is close to 2. Use a range of continuous and discrete fraction models including mixed fraction models
Thirding and fifthing partitioning strategies through paper folding (kinder squares and streamers), cutting plasticine ‘cakes’ and ‘pizzas’, sharing collections equally (counters, cards etc), apply thinking involved to help children create their own fraction diagrams (regions) and number line representations (see Siemon (2004) Partitioning – The Missing Link in building Fraction Knowledge and Confidence. Focus on making and naming parts in the thirding and fifthing families (e.g. 5 parts, fifths) including mixed fractions (e.g. “2 and 5 ninths”) and informal recording (e.g. 4 fifths), no symbols. Revisit key fraction generalisations (see Level 2), include whole to part models (e.g. partition to show 3 quarters) and part to whole (e.g. if this is 1 third, show me the whole) and use diagrams and representations to rename related fractions
Extend partitioning strategies to construct number line representations. Use multiple fraction representations
Key fraction generalisations – equal parts, as the number of parts increase the size of the part gets smaller; the number of parts names the part (e.g., 8 parts, eighths) and the size of the part depends upon the size of the whole
Zone Description
Strategy Exploring
Solves more familiar multiplication and division problems involving two-digit numbers.
For example: Butterfly House parts c and d • Packing Pots part c • Speedy Snail part a. Tends to rely on additive thinking, drawings and/or informal strategies to tackle problems involving larger numbers and/or decimals and less familiar situations.
For example: • Packing Pots part d • Filling the Buses parts a and b • Tables & Chairs parts g and h • Butterfly House parts h and g • Speedy Snail part c • Computer Game part a • Stained Glass Windows parts a and b. Tends not to explain their thinking or indicate working. Able to partition given number or quantity into equal parts and describe part formally (for example Pizza Party parts a and b). Can locate familiar fractions (for example, Missing Numbers part a). Beginning to work with simple proportion.
For example, can make a start, represent problem, but unable to complete successfully or justify their thinking (for example, How Far part a, School Fair parts a and b).
Teaching Implications
Consolidate/establish:
See the Ideas and strategies introduced/developed in the previous Zone
Introduce/develop:
More efficient strategies for multiplying and dividing larger whole numbers
independently of models (e.g. strategies based on: doubling, renaming the number of groups, factors, place-value, and known addition facts,
for example, for dividing 564 by 8, THINK, 8 what’s are 560? 8 by 7 tens or 70, so 70 and 4 remainder.
for example, for 3908 divided by 10, RENAME as, 390 tens and 8 ones, so 390.8)
Tenths as a new place-value part, by making/representing, naming and recording ones and tenths (see Siemon et al, 2015), consolidate by comparing, ordering, sequencing counting forwards and backwards in ones and/or tenths, and renaming
How to partition continuous quantities more generally using the halving, thirding, fifthing strategies (see Siemon et al, 2015 and Siemon (2004) Partitioning – The Missing Link in building Fraction Knowledge and Confidence ), for example, recognise that sixths can be made by halving and thirding (or vice versa), tenths can be made by fifthing and halving etc, use this knowledge to construct fraction diagrams (e.g. region models) and representations (e.g. number line) for common fractions and decimals including mixed numbers
Informal, partition-based strategies for renaming simple unlike fractions, for example, recognise that thirds and fifths can be renamed by thirding and then fifthing (or vice versa) on a common diagram, for example,
 Link to region model of multiplication (in this case 3 fives, or 3 parts by 5 parts) to recognise that thirds by fifths are fifteenths, so 2 thirds (2 rows) can be renamed as 10 fifths and 4 fifths (4 columns) can be renamed as 12 fifteenths. Use partitioning strategies to informally add and subtract like and related fractions
Link to region model of multiplication (in this case 3 fives, or 3 parts by 5 parts) to recognise that thirds by fifths are fifteenths, so 2 thirds (2 rows) can be renamed as 10 fifths and 4 fifths (4 columns) can be renamed as 12 fifteenths. Use partitioning strategies to informally add and subtract like and related fractions
Key fraction generalisations – that is, recognise that equal parts are necessary, the total number of parts names the part, and as the total number of parts increases they get smaller (this idea is crucial for the later development of more formal strategies for renaming fractions (see Level 5) which relate the number of parts initially (3, thirds) to the final number of parts (15, fifteenths) in terms of factors, that is, the number of parts has been increased by a factor of 5)
Metacognitive strategies to support problem comprehension, problem representation, strategy monitoring/checking, and interpretation of outcomes relevant to context (see Siemon and Booker (1990) paper on Teaching and Learning For, About and Through Problem Solving)
Simple proportion problems that introduce techniques for dealing with these situations (e.g. find for 1 then multiply or divide as appropriate, using scale diagrams and interpreting distances from maps)
Zone Description
Strategy Refining
Systematically solves simple proportion and array problems, suggesting Multiplicative Thinking.
For example: • Butterfly House part e • Packing Pots part a • How Far part a. May use additive thinking to solve simple proportion problems involving fractions.
For example: • School Fair part a • Speedy Snail part b. Able to solve simple, twostep problems using a recognised rule or relationship (for example, Fencing the Freeway Part A). However, finds this difficult for larger numbers.
For example: • Tables & Chairs parts k and l • Tiles, Tiles, Tiles part c • Stained Glass Windows part c. Able to order numbers involving tens, ones, tenths and hundredths in supportive context.
For example, Swimming Sports part a. Able to determine all options in Cartesian product situations involving relatively small numbers, but tends to do this additively.
For example: • Canteen Capers part a • Butterfly House parts l and i. Beginning to work with decimal numbers and percent but unable to apply efficiently to solve problems.
For example, Swimming Sports parts a and b, Computer Game part b. Some evidence that multiplicative thinking being used to support partitioning.
For example, Missing Numbers part b. Beginning to approach a broader range of multiplicative situations more systematically.
Teaching Implications
Consolidate/establish:
See the Ideas and strategies introduced/developed in the previous Zone
Introduce/develop:
Place-value ideas and strategies for 5 digits and beyond if not already developed and
decimal fractions to hundredths (see partitioning below) including renaming
Flexible, meaningful and efficient strategies for multiplying and dividing by multiples of ten (e.g. 2.13 by 10, THINK, 21 ones and 3 tenths, 21.3)
The area idea to support multi-digit multiplication and formal recording (see Siemon et al, 2015) and more efficient strategies for representing and solving an expanded range of Cartesian product problems involving three or more variables and tree diagram representations
Formal terminology associated with multiplication and division such as factor, product, divisor, multiplier and raised to the power of …. Play ‘Factor Cross Game’. Use calculators to explore what happens with repeated factors, for example, 4 x 4 x 4 x 4 …, factors less than 1, and negative factors.
Informal, partition-based strategies for renaming an expanded range of unrelated fractions as a precursor to developing an efficient, more formal strategy for generating equivalent fractions (see below), for example, explore using paper folding, diagrams and line models how sixths and eighths could be renamed as forty-eighths but they can also be renamed as twenty-fourths because both are factors of 24
The generalisation for renaming fractions, that is, if the number of equal parts (represented by the denominator) increases/decreases by a certain factor then the number of parts required (indicated by the numerator) increases/decreases by the same factor
Written solution strategies for the addition and subtraction of unlike fractions, for example, think of a diagram showing sixths by eighths … forty-eighths… Is this the simplest? No, twenty-fourths will do, rename fractions by inspection
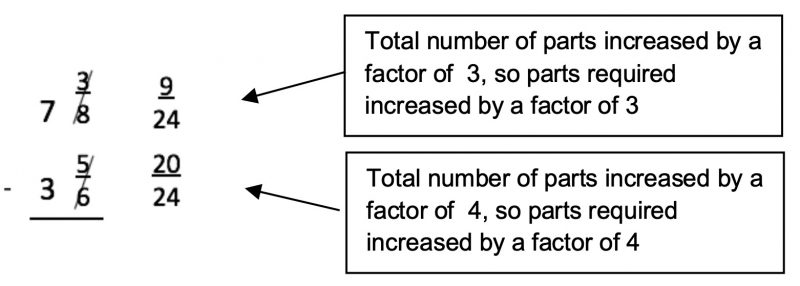
9 twenty-fourths can’t take 20 twenty-fourths, trade 1 one for 24 twenty-fourths to get 6 and 33 twenty-fourths, subtraction is then relatively straightforward
Explore link between multiplication and division and fractions including decimals (e.g. 3 pizzas shared among 4, 3 divided by 4 is 0.75 etc) to understand fraction as operator idea (e.g. 3⁄4 of 120, 75% of $48, 250% of 458,239). Use ‘Multiple Patterns Worksheet’ (See Support Materials). Establish benchmark equivalences (e.g. 1 third =33 %)
Metacognitive strategies to support problem comprehension, strategy monitoring/checking, and interpretation of outcomes relevant to context (see Siemon and Booker (1990) paper on Teaching and Learning For, About and Through Problem Solving)
Zone Description
Strategy Extending
Can work with Cartesian Product idea to systematically list or determine the number of options.
For example: • Canteen Capers part b • Butterfly House parts i and h. Can solve a broader range of multiplication and division problems involving two digit numbers, patterns and/or proportion.
For example: • Tables & Chairs part h • Butterfly House part f • Stained Glass Windows parts b and c Computer Game parts a and b. However, may not be able to explain or justify solution strategy.
For example: • Fencing the Freeway parts b and d • Swimming Sports part b • How Far part b • Speedy Snail part b. Able to rename and compare fractions in the halving family (for example, Pizza Party part c) and use partitioning strategies to locate simple fractions (for example, Missing Numbers part a). Developing sense of proportion (for example, sees relevance of proportion in Adventure Camp part a and Tiles, Tiles, Tiles part b), but unable to explain or justify thinking. Developing a degree of comfort with working mentally with multiplication and division facts.
Teaching Implications
Consolidate/establish:
See the Ideas and strategies introduced/developed in the previous Zone
Introduce/develop:
Hundredths as a new place-value part, by making/representing, naming and recording ones, tenths, and hundredths (see Siemon et al, 2015), consolidate by comparing, ordering, sequencing counting forwards and backwards in place-value parts, and renaming. Link to %
How to explain and justify solution strategies for problems involving multiplication and division (see Multiplication Workshop handout in Support Materials), particularly in relation to interpreting decimal remainders appropriate to context, for example,
How many buses will be needed to take 594 students and teachers to the school Speech night, assuming each bus hold 45 passengers and everyone must wear a seatbelt?
More efficient, systematic, and/or generalizable processes for dealing with proportion problems (e.g. use of the ‘for each’ idea, formal recording, and the use of fractions, percent to justify claims), for example,
Jane scored 14 goals from 20 attempts. Emma scored 18 goals from 25 attempts. Which girl should be selected for the school basketball team and why?
6 girls share 4 pizzas equally. 8 boys share 6 pizzas equally. Who had more pizza, the girls or the boys?
35 feral cats were found in a 146 hectare nature reserve. 27 feral cats were found in a 103 hectare reserve. Which reserve had the biggest feral cat problem?
Orange juice is sold in different sized containers: 5L for $14, 2 L for $5, and 500mL for $1.35. Which represents the best value for money?
More efficient strategies and formal processes for working with multiplication and division involving larger numbers based on sound place-value ideas, for example, 3486 x 21 can be estimated by thinking about 35 hundreds by 2 tens, 70 thousands, and 1 more group of 35 hundred, that is, 73,500, or it can be calculated by using factors of 21, that is, 3486 x 3 x 7. Two-digit multiplication can be used to support the multiplication of ones and tenths by ones and tenths, for example, for 2.3 by 5.7, rename as tenths and compute as 23 tenths by 57 tenths, which gives 1311 hundredths hence 13.11. Consider a broader range of problems and applications, for example,
Average gate takings per day over the World Cricket cup Series
Matt rode around the park 8 times. The odometer on his bike indicated that he ridden a total of 15 km. How far was it around the park?
After 11 training sessions, Kate’s average time for 100 metres butterfly was 61.3 seconds. In her next 2 trials, Kate clocked 61.21 and 60.87 seconds. What was her new average time?
Integers using real-world examples such as heights above and below sea-level, temperatures above and below zero, simple addition and difference calculations
The notion of variable and how to recognise and formally describe patterns involving all four operations. Use ‘Max’s Matchsticks’ to explore how patterns may be viewed differently leading to different ways of counting and forms of representation.
Zone Description
Connecting
Able to solve and explain one-step problems involving multiplication and division with whole numbers using informal strategies and/or formal recording.
For example: • Filling the Buses part a • Fencing the Freeway part d • Packing Pots part d. Can solve and explain solutions to problems involving simple patterns, percent and proportion.
For example: • Fencing the Freeway part c • Swimming Sports part b • Butterfly House part g • Tables & Chairs parts g and l • Speedy Snail part c • Tiles, Tiles, Tiles parts b and c • School Fair part a • Stained Glass Windows part a • Computer Game part b • How Far part b. May not be able to show working and/or explain strategies for situations involving larger numbers.
For example: • Tables & Chairs parts m and k • Tiles, Tiles, Tiles part c. May not be able to show working and/or explain strategies for less familiar problems.
For example: • Adventure Camp part b • School Fair part b • How Far part c. Locates fractions using efficient partitioning strategies.
For example, Missing Numbers part a. Beginning to make connections between problems and solution strategies and understand how to communicate this mathematically.
Teaching Implications
Consolidate/establish:
See the Ideas and strategies introduced/developed in the previous Zone
Introduce/develop:
Strategies for comparing, ordering, sequencing, counting forwards and backwards in place-value parts, and renaming large whole numbers, common fractions, decimals, and integers (e.g. a 3 to 4 metre length of rope, appropriately labelled number cards and pegs could be used to sequence numbers from 100 to 1,000,000, from -3 to +3, from 2 to 5 and so on). The metaphor of a magnifying glass can be used to locate numbers involving hundredths or thousandths on a number line as a result of successive tenthing (see Siemon et al, 2015 and Siemon (2004) Partitioning – The Missing Link in building Fraction Knowledge and Confidence )
An appreciation of inverse and identity relations, for example, recognise which number when added leaves the original number unchanged (zero) and how inverses are determined in relation to this, for example, the inverse of 8 is -8 as -8 + 8 = 0 and 8 + -8 = 0. In a similar fashion, recognise that 1 is the corresponding number for multiplication, where the inverse of a number is defined as its reciprocal, for example, the inverse of 8 is 1/8
Index notation for representing multiplication of repeated factors, for example,
5 x 5 x 5 x 5 x 5 x 5 = 56
A more generalised understanding of place-value and the structure of the number system in terms of exponentiation, for example,
10-³, 10-², 10-¹, 100, 10¹, 10² 10³ …
Strategies to recognise and apply multiplication and division in a broader range of situations including ratio, proportion, and unfamiliar, multiple-step problems, for example, Orange Juice task (see Support Materials)
How to recognise and describe number patterns more formally for example, triangular numbers, square numbers, growth patterns (e.g. ‘Garden Beds’ from Maths 300 and ‘Super Market Packer’ from Support Materials)
Notation to support general arithmetic (simple algebra), for example, recognise and understand the meaning of expressions such as
x+4, 3x, 5x²,or (x-1)/3
Ratio as the comparison of any two quantities, for example, the comparison of the number of feral cats to the size of the national park. Recognise that ratios can be used to compare measures of the same type (e.g. the number of feral cats compared to the number of feral dogs) and that within this, two types of comparison are possible, for instance, one can compare the parts to the parts (e.g. cats to dogs) or the parts to the whole (e.g. cats to the total number of cats and dogs). Ratios can be also used to compare measures of different types, when used this way they are referred to as rates (e.g. the number of feral cats per square kilometre). Ratios are not always rational numbers (e.g. the ratio of the circumference of a circle to its diameter)
Strategies for recognising and representing proportion problems involving larger numbers and/or fractions (e.g. problems involving scale such as map calculations, increasing/reducing ingredients in a recipe, and simple problems involving derived measures such as volume, density, speed, and chance)
Zone Description
Reflective Knowing
Can use appropriate representations, language and symbols to solve and justify a wide range of problems involving unfamiliar multiplicative situations including fractions and decimals.
For example: • Adventure Camp part b • Speedy Snail part b. Can justify partitioning.
For example, Missing Numbers part b.Can use and formally describe patterns in terms of general rules.
For example, Tables and Chairs, parts m and k. Beginning to work more systematically with complex, open-ended problems.
For example: • School Fair part b • Computer Game part c.
Teaching Implications
Consolidate/establish:
See the Ideas and strategies introduced/developed in the previous Zone
Introduce/develop:
A broader range of multiplicative situations for example, problems involving the calculation of area or volume, derived measures and rates, variation, complex proportion, and multiple step problems involving large whole numbers, decimals and fractions, for example,
Find the volume of a cylinder 4 cm in diameter and 9 cm long.
Find the surface area of a compound shape
Foreign currency calculations
Determine the amount of water lost to evaporation from the Hume Weir during the summer.
Strategies for simplifying expressions for example, adding and subtracting like terms, and justifying and explaining the use of cancellation techniques for division through the use of common factors, for example,
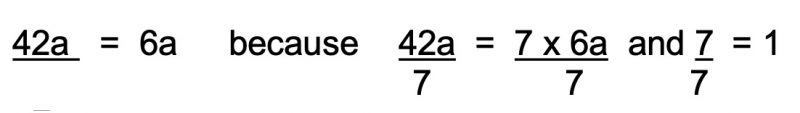 Algebraic reasoning and representation strategies to solve problems involving multiplicative relationships, for example,
Algebraic reasoning and representation strategies to solve problems involving multiplicative relationships, for example,
If 2 T-shirts and 2 drinks cost $44 and 1 T-shirt and 3 drinks cost $30, what is the price of each?
5 locker keys are returned at random to the students who own them. What is the probability that each student will receive the key that opens their locker?
A mad scientist has a collection of beetles and spiders. The sensor in the floor of the enclosure indicated that there were 174 legs and the infra-red image indicated that there were 26 bodies altogether. How many were beetles and how many were spiders?
365 is an extraordinary number. It is the sum of 3 consecutive square numbers and also the sum of the next 2 consecutive square numbers. Find the numbers referred to.
Strategies for working with numbers and operations expressed in exponent form, for example, why 23 x 26 = 29, investigate the structure of the place value system in terms of positive and negative powers of 10
Explore non-linear, exponential situations such as growth and decay (e.g. Radioactivity activity from maths300)
Writing mathematically using appropriate symbolic text, using equivalent sentences to systematically arrive at a solution
More abstract problem solving situations requiring an appreciation of problem solving as a process, the value of recognising problem type, and the development of a greater range of strategies and representations (e.g. tables, symbolic expressions, rule generation and testing) including the manipulation of symbols
Mapping to the Australian Curriculum: Mathematics
LAF ZONES (Siemon et al., 2006) |
LINKS TO ACARA (2015) |
|---|---|
Zone 1:
Multiplicative thinking (MT) not really apparent as no indication that groups are perceived as composite units, dealt with systematically, or that the number of groups can be manipulated to support more efficient calculation. |
Foundation Year:
Problem Solving: use familiar counting sequences to solve unfamiliar problems. Year 1:
Problem Solving: use familiar counting sequences to solve unfamiliar problems. Year 2:
|
Zone 2:
Some evidence of MT as equal groups/shares seen as entities that can be counted. |
Year 2:
Understanding: connecting number calculations with counting sequences and partitioning and combining numbers flexibly. Fluency: counting numbers in sequences readily. Year 3:
Understanding: partitioning and combining numbers flexibly and representing unit fractions Fluency: recalling multiplication facts |
Zone 3:
Beginning to work with larger whole numbers and patterns but tends to rely on count all methods or additive thinking (AT). |
Year 4:
Problem Solving: using properties of numbers to continue patterns Reasoning: using generalising from number properties and results of calculations and deriving strategies for unfamiliar multiplication and division tasks |
Zone 4:
|
Year 4:
Understanding: partitioning and combining numbers flexibly Year 5:
Understanding: comparing and ordering fractions and decimals and representing them in various ways Problem Solving: formulating and solving authentic problems using whole numbers |
Zone 5:
|
Year 5:
Reasoning: investigating strategies to perform calculations efficiently and continuing patterns involving fractions and decimals Year 6:
Fluency: calculating simple percentages, converting between fractions and decimals, and using operations with fractions, decimals and percentages Problem Solving: formulating and solving authentic problems using fractions, decimals and percentages |
Zone 6:
Developing capacity to work mentally with multiplication and division facts |
Year 6:
Understanding: representing fractions and decimals in various ways and describing connections between them Reasoning: explaining mental strategies for performing calculations Year 7:
Fluency: calculating accurately with integers and representing fractions and decimals in various ways Problem Solving: formulating and solving authentic problems using numbers |
Zone 7:
|
Year 7:
Understanding: describing patterns in uses of indices with whole numbers, and connecting the laws and properties of numbers to algebraic terms and expressions Fluency: calculating accurately with integers and representing fractions and decimals in various ways Problem Solving: formulating and solving authentic problems using numbers Reasoning: applying the number laws to calculations and applying an understanding of ratio Year 8:
Understanding: identifying commonalities between operations with algebra and arithmetic. |
Zone 8:
|
Year 8:
Understanding: describe patterns involving indices, connecting rules for linear relations and their graphs. Fluency: includes formulating, and modelling practical situations involving ratios, profit and loss, and areas and perimeters of common shapes. Year 9:
Understanding: describe the relationship between graphs and equations. Fluency: applying the index laws to expressions with integer indices. |
Mapping to the National Numeracy Learning Progression
LAF ZONES (Siemon et al., 2006) |
LINKS TO ACARA (2015) |
|---|---|
Zone 1:
Multiplicative thinking (MT) not really apparent as no indication that groups are perceived as composite units, dealt with systematically, or that the number of groups can be manipulated to support more efficient calculation. |
Foundation Year:
Problem Solving: use familiar counting sequences to solve unfamiliar problems. Year 1:
Problem Solving: use familiar counting sequences to solve unfamiliar problems. Year 2:
|
Zone 2:
Some evidence of MT as equal groups/shares seen as entities that can be counted. |
Year 2:
Understanding: connecting number calculations with counting sequences and partitioning and combining numbers flexibly. Fluency: counting numbers in sequences readily. Year 3:
Understanding: partitioning and combining numbers flexibly and representing unit fractions Fluency: recalling multiplication facts |
Zone 3:
Beginning to work with larger whole numbers and patterns but tends to rely on count all methods or additive thinking (AT). |
Year 4:
Problem Solving: using properties of numbers to continue patterns Reasoning: using generalising from number properties and results of calculations and deriving strategies for unfamiliar multiplication and division tasks |
Zone 4:
|
Year 4:
Understanding: partitioning and combining numbers flexibly Year 5:
Understanding: comparing and ordering fractions and decimals and representing them in various ways Problem Solving: formulating and solving authentic problems using whole numbers |
Zone 5:
|
Year 5:
Reasoning: investigating strategies to perform calculations efficiently and continuing patterns involving fractions and decimals Year 6:
Fluency: calculating simple percentages, converting between fractions and decimals, and using operations with fractions, decimals and percentages Problem Solving: formulating and solving authentic problems using fractions, decimals and percentages |
Zone 6:
Developing capacity to work mentally with multiplication and division facts |
Year 6:
Understanding: representing fractions and decimals in various ways and describing connections between them Reasoning: explaining mental strategies for performing calculations Year 7:
Fluency: calculating accurately with integers and representing fractions and decimals in various ways Problem Solving: formulating and solving authentic problems using numbers |
Zone 7:
|
Year 7:
Understanding: describing patterns in uses of indices with whole numbers, and connecting the laws and properties of numbers to algebraic terms and expressions Fluency: calculating accurately with integers and representing fractions and decimals in various ways Problem Solving: formulating and solving authentic problems using numbers Reasoning: applying the number laws to calculations and applying an understanding of ratio Year 8:
Understanding: identifying commonalities between operations with algebra and arithmetic. |
Zone 8:
|
Year 8:
Understanding: describe patterns involving indices, connecting rules for linear relations and their graphs. Fluency: includes formulating, and modelling practical situations involving ratios, profit and loss, and areas and perimeters of common shapes. Year 9:
Understanding: describe the relationship between graphs and equations. Fluency: applying the index laws to expressions with integer indices. |